風倒木の力学
技術士(応用理学)横井和夫
先日、京都府宇治市在住のある人から依頼がありました。昨年(2019年)台風19号で隣家の杉が倒れて自宅の自動車を潰された。その損害賠償を要求したところ相手が応じないので裁判になった。弁護士に相談すると、必ず倒壊するという証明がないと裁判は難しいらしい。そこでインターネットで調べると筆者の記事にヒットしたので相談にきたというのである。
依頼者によるとこの木は以前からよく揺れて危ないので伐採を要求していたらしいが、隣家がそれになかなか応じなかったいう経緯もある。依頼者は樹高や枝の長さ等計算に必要な諸元は調べていたので、それに基づいて風速をいくらか変えて計算したところ、風速10m/secでOK、11m/secでギリギリ、12m-secでOUTという結果になった。依頼者によると当日の風速は10m/secぐらいではなかったかというから、計算結果とドンピシャだった。私の方法もまんざらではないと云結果でした。
(20/07/02)
風倒木の原因は何か? 鹿が食い散らかしたからか、酸性雨が原因か? それはなかなか悩ましい問題であるらしい。木が倒れるということは、一つの力学的現象に他ならない。筆者は植物生態学も、動物生態学も素人であるが、理工学を学んだ技術者の端くれとして、この種の問題にいささか興味を覚える。又、倒木が発生する条件を力学的に検討することは、単にこの現象を定量化するだけでなく、今後自然環境の現地調査を行う上でも、背後知識として持っておれば損はしない、と思われるので、この問題を一度整理しておきたい。
1)
解析モデル
風にさらされた樹木の力学モデルを下図のように仮定する。
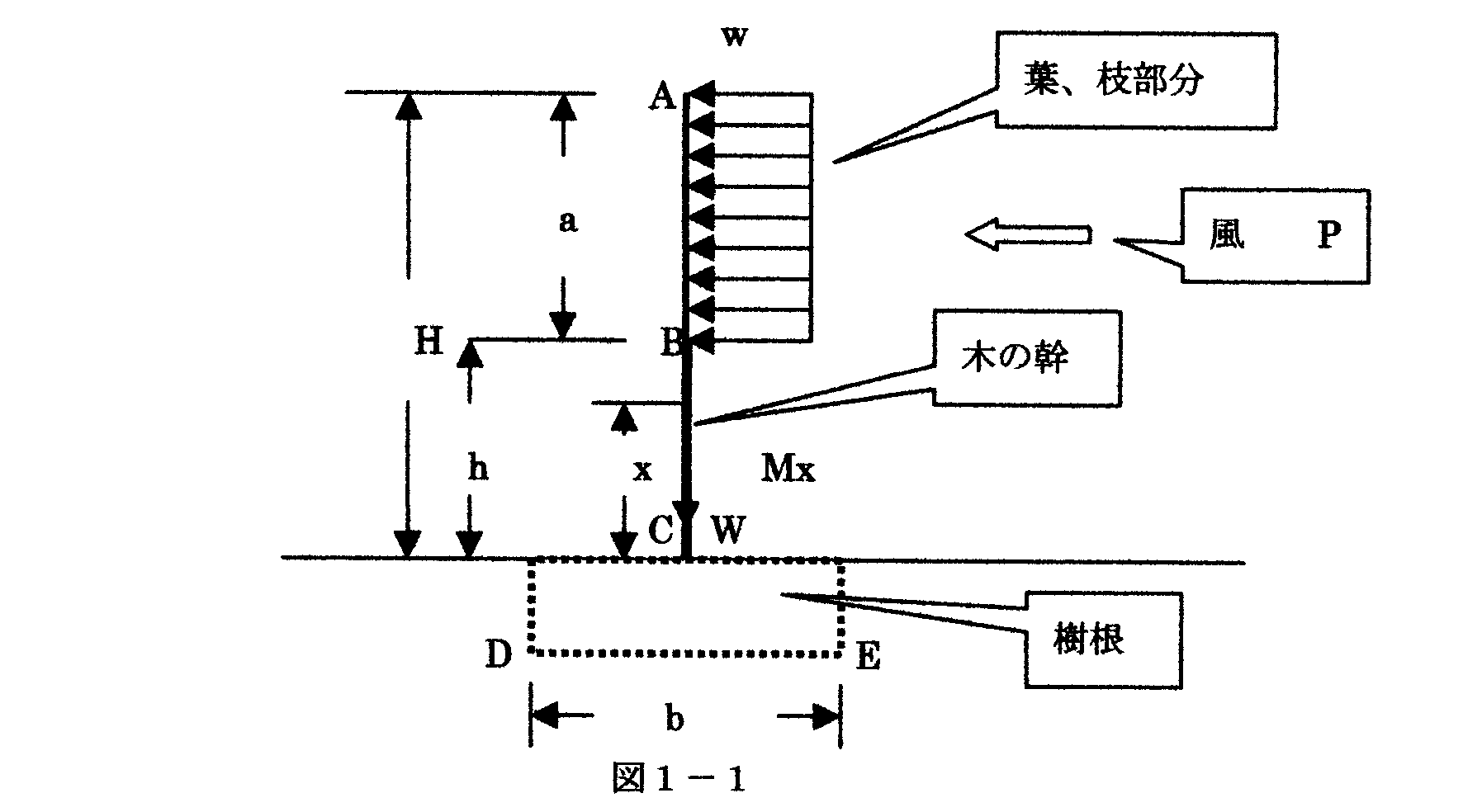
ここで、
(1) H;樹高
(2) a;葉・枝が成長している部分の長さ(この部分で風を受け止める)
(3) W:木の自重
(4) w;風圧力
(5) x;地上面からの高さ
(6) Mx;地上面からxの位置でのモーメント
2) 倒壊条件
構造力学の場では、構造物の倒壊条件として、通常次の4ケースを考える。
(1)
転倒、滑動
(2) 支持
(3) 曲げ
(4)
剪断
一般に、樹木は地下深く根を下ろしているので、(1)転倒・滑動という現象は考えがたい。又、木の繊維は縦(成長)方向に発達するから、横からの力には強い。従って、(4)剪断も考えがたい。つまり、(2)支持、(3)曲げの両者についてのみ考えれば良いだろう。
(2)支持について
構造物が立っていると、それが発生する力と同じだけの反力が地盤内に発生する。これが、地盤支持力を上回ると、支持力が低下して、傾いたり、最悪の場合、倒壊に至る。
風が吹くと、木に水平方向の力が作用する。一方、木の自重による鉛直力が働き、これらの合力が地盤に作用する。
合力の作用点と、木の中心からの距離をe、地盤に発生する反力をRA,RBとすると、両者の関係は概ね下図のように示される。
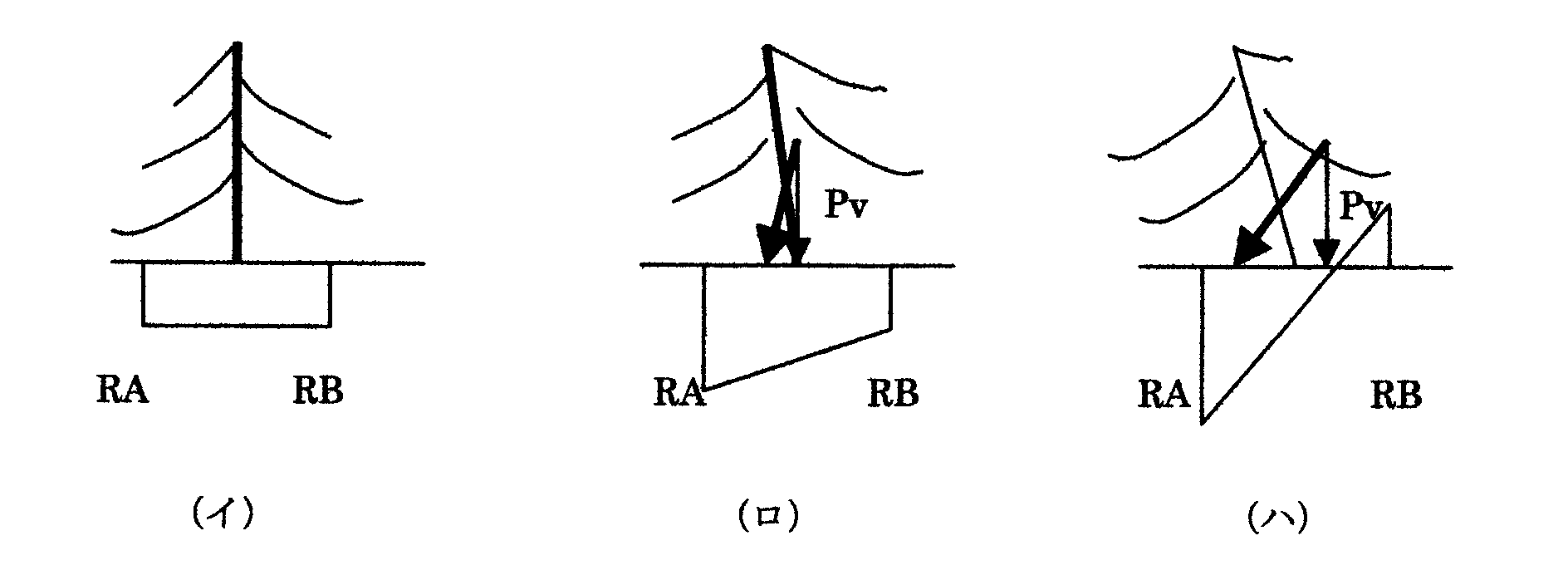
(イ)
は風のない場合で、無論e=0。RA=RB=W/2
(ロ)
は、やや強い風が吹く場合で、合力の作用点位置はやや風下に移動。地盤反力分布は図のように台形分布をとる。
ここで、e≦b/3の時、 RA=((W+Pv)/b)(1+6e/b)
RB=((W+Pv)/b)(1-6e/b)
Pv;合力の鉛直方向成分
この場合、構造系は全体として安定を保っているが、最大地盤反力RAが、地盤支持力を上回ると、地耐力不足を生じ、傾斜あるいは倒壊を生じる。
(ハ)
はもっと強い風が吹いた時で、合力の作用点位置は大きく風下にシフトする。e>b/3
となり、最大地盤反力は次式で表される。
RA=2(W+Pv)/3(b-e)
RAが地盤支持力を上回れば、傾斜又は倒壊を生じる。
ところで、大阪沿岸の埋め立て地のような軟弱地盤でもない限り、支持力不足で木が倒壊することは殆どあり得ない。
問題は(ハ)のケースで、水平力(風力)が限界以上になると、風上側に引き抜き力が発生する。この時、引き抜き力が、根の引き抜き抵抗を上回ると、倒壊を生じる。これには次の2パターンが考えられる。
①
引き抜き力が、根と土との摩擦抵抗よりも大きく、樹根部を含む全体から倒壊するケース。いわゆる「根返し」という現象が、これに該当すると思われる。
②
全体の引き抜き力は、根一本一本に対して、引っ張り応力として作用する。引っ張り応力が、根の引っ張り強度を上回ると、根は破断を起こす。一本がこれで切れると、他の根が負担する引っ張り力が大きくなるので、根は次々と破断を連鎖反応的に起こす。結果として倒壊を生じる。
大台ヶ原のような場所では、岩盤が浅い位置(地下数mないし数10㎝)に分布するため、支持力不足よりは、引き抜き抵抗不足による倒壊の方が起こりやすいと考えてよい。何故なら、岩盤が浅いと、根が深くまで成長出来ず、横に広がるばかりで、引き抜き抵抗が不足するためである。
(3) 曲げ
では、「根」がしっかり張っていて、少々の風にびくともしなかったとき、倒壊は生じないだろうか? そんなことはない。この場合、生じるのは、木があるところからぼっきりと折れる現象である。これの主役は「モーメント」という力である。木に風が作用したとき、幹の各部に曲げモーメントという力が発生します。図1-1のモデルで、地上からxの位置での曲げモーメントは次式で表される。
Mx=w・a(H-a/2-x) ………………(3.1)
意外に簡単な式です。最大曲げモーメント発生位置はx=0、つまり根元ということになる。曲げモーメントにより、幹の内部に曲げ応力が発生する。
σ=Mx/Z+We/Ae
………………………………(3.2)
σ;曲げ応力
Z;断面係数
We;着目する点から上の木の全重量
Ae;木の断面積
ここで、第2項も含めると、話しがややこしくなるので、第一項のみを取り上げる。
曲げ応力σが、木の曲げ強度σaより大きくなると、幹は曲げ破壊を起こす。ここで、Zは部材の性質とは無関係に幾何形状だけで決まり、単純円の場合
Z=(π/32)D3
………………………………(3.3)
(3.1)
(3.3)式を(3.2)に代入すると
σ=
{w・a(H-a/2-x)}/{(π/32)D3 }
…………(3.4)
D;木の直径
もし、木の根元から末端まで、直径が同じだったら、最大曲げ応力と最大曲げモーメントの発生位置は、同じx=0になるので、木は全て根元から折れるはずである。しかし、自然界にそんな木はない。大概は根元から末端にかけて細くなる。
ここで、木の直径低減率を次式で定義する。
n=(D0-D)/x
n;直径低減率
D0;樹幹部の直径
D;地表からxの位置での直径
樹高をH、木の末端での直径をDeとすると、nは次式で表される。
n=
(H-x)(D0-De)/H+De
これを3.4式に代入すると、木の各部での曲げ応力を求める一般式が得られる。ところがこの式は、nの値で振動するので、いくら式を眺めていても、この辺りで木が折れそうだ、ということがなかなか判らない。実際に、木はどこから折れるかは、判らないのだが、おそらく最大曲げ応力が発生する場所が、一番折れやすく、そこから順番に破壊が進行して行くだろうと、予測される。そこで、ある条件を仮定して、数値計算で木に発生する曲げ応力の分布を調べてみた。
今回は次のような条件を設定した。
〇樹高 H=30m
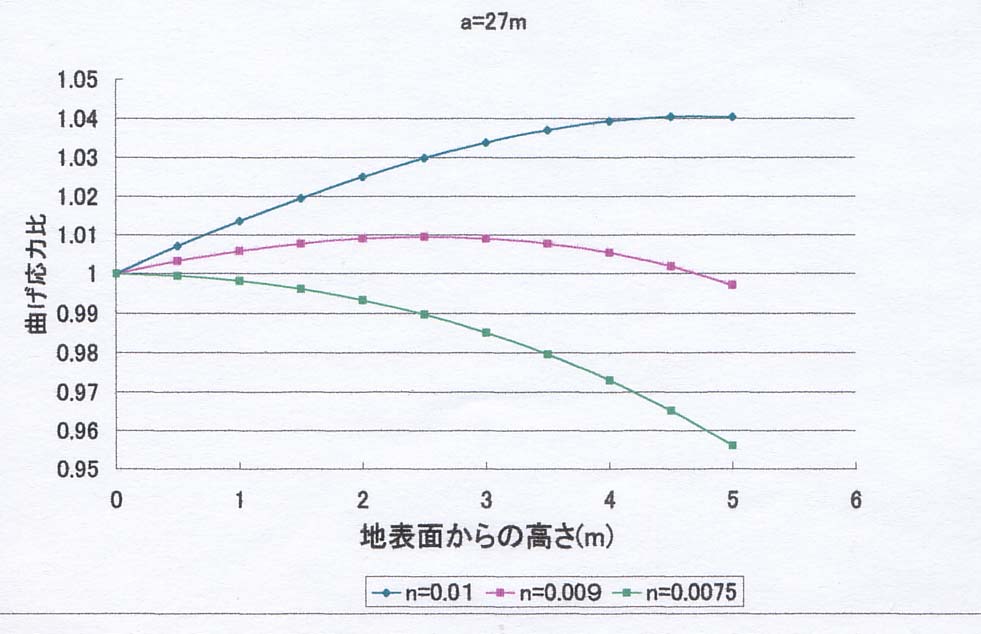
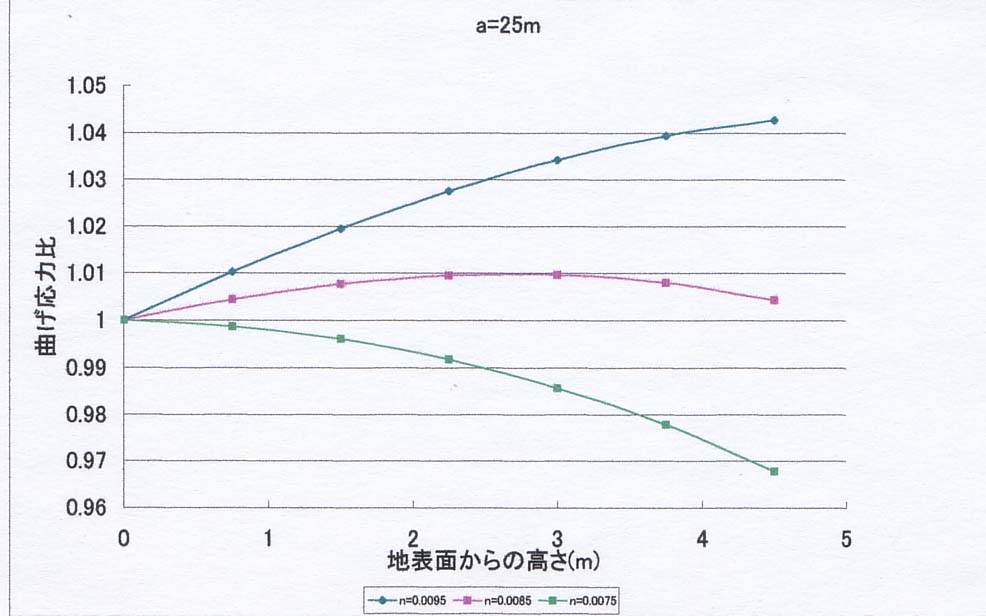
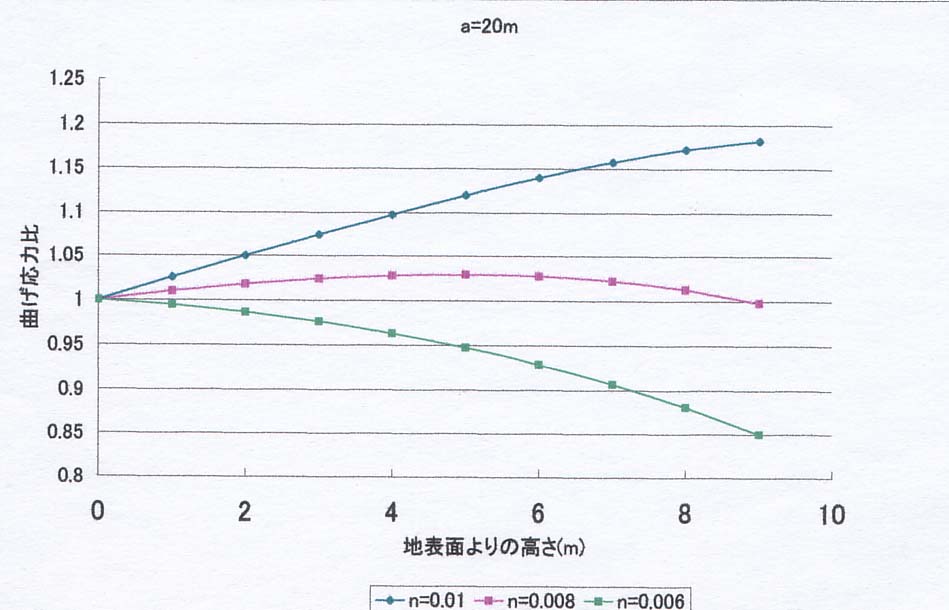
〇樹幹部 図1.1のBC間の距離 3m(a=27m)、5m(a=25m)、10m(a=20m)
〇幹の直径 D0=0.3m(これは結果に影響しないので幾らでも構わない)
〇直径の低減率n
パラメーター
結果を下図に示します。この図では、x=0(樹幹)での曲げ応力を1とし、それとの比率を、nをパラメーターにして、表しています。
1) どのケースでも、直径低減率nによって、最大曲げ応力発生パターンは大きく異なる。
2) nが概ね0.09以上になると、高さに伴って、曲げ応力は増大し、B点付近で最大になる。つまり、B点付近から折れやすくなる(筈である)。実際、この部分の上下で、木全体の断面係数や、風による振動特性が大きく異なるため、応力集中が生じることは容易に予測される。
3)
nが概ね0.07以下になると、曲げ応力は単純に減少し、X=0の位置で曲げ応力が最大になる。つまり、根元から折れる。このケースは根元から末端まで、余り直径が変わらない、というケースであり、自然界でそのような木が在るのか、疑問である。
4)
nが概ね0.08前後では、BC間で応力分布が極値を持つ。つまり、途中から折れるケースである。しかし、試算によれば、これはnが極めて狭い範囲にあるケースにのみ見られ、現実的なものかどうか、疑問である。
つまり、通常の条件で、曲げ破壊が最も生じやすいのは、図1.1のB点付近で、これより上は、むしろ曲げ破壊は起こり難い。又、これより下の位置で折損が起こったとすると、それは極めて珍しい例か、又は何らかの原因による断面欠損が考えられる。式3.3を見ても判るように、断面係数Zは直径Dの三乗に比例するから、Dが僅か減少しただけで、曲げ応力は大きく増大する。従って、見た目では僅かな断面欠損でも、構造力学上は無視できない。そいう意味で、客観的に見たとき、鹿害も選択肢の一つに入れざるを得ないだろう。
但し、木の曲げ破壊は、現実にはかなり確率的な現象であり、以上の推論が、決定論的に、全てに当てはまるとは思わない。しかし、一つの傾向を示しているのではないか、と考えられる。従って、風倒木に対する現地調査では、以上の検討結果を頭に入れておけば、対策工を考える上で有効と考えている。
4)対策工
4.1)根返しに対して
これの原因は、風による引き抜き力に対し、引き抜き抵抗力が不足していることである。対策としては、大きく、次の2方向がある。
(1)引き抜き力を低減する
(2)引き抜き抵抗力を付加する。
(1)引き抜き力を低減する
木に働く水平モーメントを低減すればよい。木の高さを調節して、重心を低くすれば、水平モーメントは小さくなる。木の風害防止によく行われるのは、下枝伐採だが、これは逆で、木の高さがある程度以上になれば、高くなった部分を伐採した方が、効果的である。
(2)引き抜き抵抗力を付加する。
不足する引き抜き抵抗力を人口的に付加する。最も考えやすいのは、支柱で支えるとか、ワイヤーで引っ張るとかであるが、いかにも脳がない。また、この種の人工構造物は、周辺環境との調和性という点で、国立公園内施設にふさわしくない。更に、これらの工法は、部材が全て既製鉄工品であるため、儲けは皆メーカーや商社が持っていき、更に実際の製造発注は、中国辺りに流れるので、国内や地域業者にとって、メリットは何もない。喜ぶのはムネオ的議員とムネオ向き商社だけ。
最も効果的で且つ安価なのは、「押さえ盛土工法」である。幹を中心に数mの範囲を0.3~1.0mの高さで盛土を行う。これだけで十分な効果がある。
①
材料の土は周辺や県内の、土木・建築工事で発生する建設残土を使用すれば、経費は運搬・盛り立て費だけ。
②
大台ヶ原という雨の多い地域性を考えると、押さえ盛土の崩壊・流出が懸念されるが、それを生じさせないような、盛土構造・盛土工法にすればよい。これは大して難しくはない。環境調和性を考えると、有機材(強化澱粉など)を用いた補強土工法とか、偽岩を用いた簡易擁壁工などが考えられる。
③
盛土表面を現地種で植生すれば、環境調和性にも問題はない。
④ 工事そのものは簡単なので、要領さえ呑み込めば、地元業者で十分対応可能。
⑤
引き抜きによる倒壊が生じるのは、実は岩盤が浅い場合である。岩盤が浅いと、根は深くまで成長出来ず、地表に沿って横に広がるだけになる。これでは引き抜き抵抗は期待出来ない。従って、対策工の計画・設計には対象樹木直下での、岩盤の深さを調査する必要がある。簡易貫入試験・表面波探査法などの適用が考えられる。
4.2)曲げ破壊について
これが発生するのは、外力に対して、木の断面が不足しているためである。木の断面不足をどの様にして補充するのか。橋脚なら、鉄板で巻くのが、通常用いられている工法だが、生木に鉄板を巻く訳にも行かないだろう。又、将来動物による断面欠損が懸念されるなら、現在用いられている、ラス巻きも、これでOKとは云わないが、やらないよりまし程度の効果は期待出来るだろう。問題は、今後折損する可能性のある木がどれぐらいあるか、を予測することである。
その手法の一つとして、曲げ応力の予測計算が挙げられる。今回、紹介した計算は、あくまで当たり計算である。これに対象樹木の許容曲げ強度、予測風圧力を与えれば、具体的な予測計算が可能になります。この方法は、倒木の高さと、直径を数カ所で測れば良い(道具としては梯子とメジャー・コンベックスがあればよい)ので、誰でも簡単に出来ます。又、この計算は全然難しくなく、エクセルで簡単に出来ます。希望があれば、計算コードを公開します。
Newsへ